
TypeScript에서는 BigDecimal 타입은 따로 존재하지 않습니다.
BigDecimal 타입을 사용하는 이유에 대해서 포스트를 작성하게 된 계기는 Java 언어에서 화폐 단위, 비율 계산 등으로 인해 BigDecimal 타입을 사용하는 것을 보고 BigDecimal 타입이 무엇인지? 왜 사용하는지 궁금해서 포스트를 작성하게 됐습니다.
Java 언어에서는 숫자를 정밀하게 저장하고 표현할 수 있는 타입으로 BigDecimal 타입을 사용합니다.
소수점을 표현하기 위해 float, double 타입을 사용하는데 float, double 타입으로 사용하지 않고 BigDecimal 타입을 사용하는 이유는 화폐에서 환율 그리고 비율(금액, 퍼센트 할인) 계산 등 소수점까지 정확히 표현해야 하기 때문인데, float, double의 실수형 타입에 대한 부동소수점의 부정확성을 고려하여 정확한 계산 값을 표현하기 위해서 사용합니다.
✔ BigDecimal
JavaScript 원시형 타입에는 숫자를 표현할 수 있는 타입이 2개가 있는데 대부분의 경우 number를 사용합니다.
숫자형(Number Type)은 정수 및 부동 소수점 숫자(Floating Point Number)를 표현합니다.
부동 소수점 같은 경우 컴퓨터에서 부동 소수점을 표현하는 가장 널리 쓰이는 표준(IEEE 754) 규격을 사용하고 있습니다.
컴퓨터는 소수를 2진수를 이용해 저장하기 때문에, 10진수 소수를 정확히 다룰 수 없습니다. 2진수의 근사치를 표현하기 때문에 어느 정도의 오차가 존재하고 이를 반올림 오차(rounding error)라고 하고, 다른 프로그래밍 언어에서도 반올림 오차가 존재합니다.
이런 오차를 그냥 놔두는 이유는 계산 상의 효율성을 위한 것입니다. 컴퓨터의 저장용량은 한정되어 있고 내부적으로 0, 1밖에 다룰 수 없으므로, 이런 제약 아래에서 10진수 소수를 아주 빠르게 계산하기 위해서 컴퓨터 설계자들이 이런 선택을 한 것입니다.
let n1: number = 2.0;
let n2: number = 0.2;
for(let i: number = 0; i < 3; i++) {
d1 += d2;
console.log(d1);
}
// 2.2
// 2.4000000000000004
// 2.6000000000000005
const a: number = 0.1;
const b: number = 0.2;
console.log(a+b);
// 0.30000000000000004
console.log((a+b) == 0.3);
// false위와 같은 문제로 정확한 숫자(금액 계산)를 표현하기 위해서 big.js, decimal.js 등의 라이브러리를 사용합니다.
위와 같은 문제가 발생하는 부동소수점에 대해서 좀 더 살펴보겠습니다.
✔ 부동 소수점
부동소수점은 실수를 컴퓨터상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로, 유효숫자를 나타내는 가수와 소수점의 위치를 풀이하는 지수로 나누어 표현합니다.
부동소수점에 대해 얘기하기 앞서 컴퓨터에서 실수를 표현하는 방식에 대해 얘기해보겠습니다.
컴퓨터의 실수 표현
컴퓨터에서 실수를 표현하는 방법은 정수에 비해 훨씬 복잡합니다. 컴퓨터에서는 실수를 정수와 마찬가지로 2진수로만 표현해야 하기 때문입니다. 현재에는 다음과 같은 방식이 사용되고 있습니다.
- 고정 소수점(Fixed Point) 방식
- 부동 소수점(Floating Point) 방식
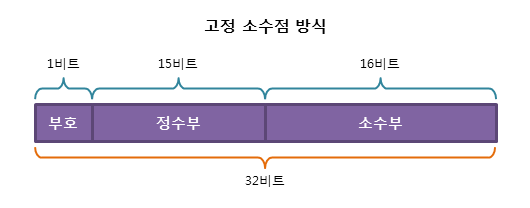
고정 소수점(Fixed Point) 방식
고정 소수점 방식은 정수부와 소수부의 자릿수를 미리 정해놓고 고정된 자릿수의 소수를 표현하는 것입니다.
7.625라는 실수를 2진수로 변환하면 111.101이 됩니다.

맨 앞 1자리는 부호 비트(Sign Bit)이고 0이면 양수, 1이면 음수로 표현합니다.
나머지 비트들은 소수점을 기준으로 정수부와 소수부를 표현하는데 소수점을 기준으로 앞에서부터 채우고 남는 뒷자리는 0으로 채운다. 고정소수점 방식은 소수점이 고정되어 있기 때문에 구현하기 편리하지만 자릿수가 크지 않으므로, 표현할 수 있는 범위가 매우 적다는 단점이 있습니다.
10진수를 2진수로 변환하는 방법
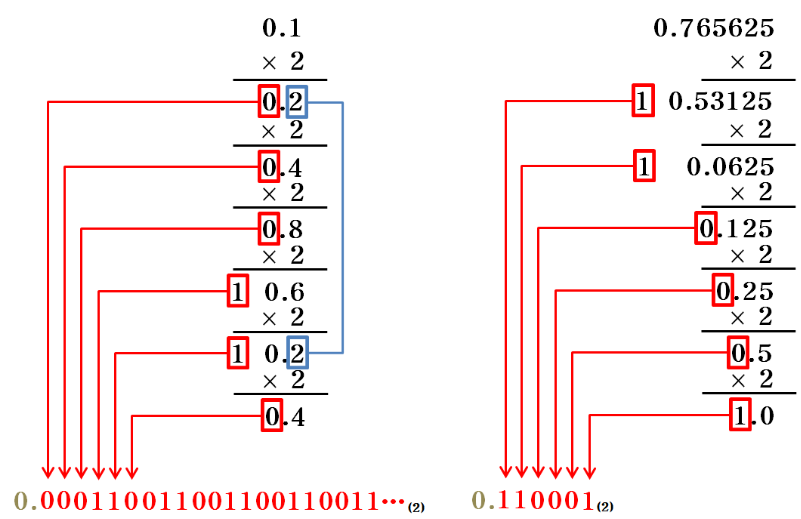
정수 10진수를 2진수로 변환하는 방법은 2를 나눈 나머지의 값을 구하고 밑에서부터 거꾸로 읽으면 됩니다.
소수점 10진수를 2진수로 변환하는 방법은 2를 곱해서 0으로 떨어질 때까지 곱해주면 됩니다.
부동 소수점(Floating Point) 방식
부동 소수점 방식은 소수점의 위치가 바뀌기 때문에 실수를 표현할 때 주로 사용하며 고정 소수점 방식보다 넓은 범위의 수를 표현할 수 있습니다. 부동 소수점 방식은 표현 범위에 따라 4Byte의 단정도(Single Precision) 부동 소수점 형식과 8Byte의 배정도(Double Precision) 부동 소수점 형식으로 나눌 수 있습니다.
단정도 부동 소수점 형식은 부호 1bit, 지수 8bit, 가수 23bit인 32bit를 할당합니다.
배정도 부동 소수점 형식은 부호 1bit, 지수 11bit, 가수 52bit인 64bit를 할당합니다.


부동 소수점 변환 예시로는 32비트 단정도 부동 소수점 형식으로 얘기하겠습니다.
IEEE 754의 부동 소수점 표현은 크게 세 부분으로 구성되는데 최상위 비트는 부호를 표시하고 지수부(Exponent)와 가수부(Fraction/Mantissa)가 있습니다.
부동 소수점 x는 다음 형태를 가집니다.
x = (-1)^s * m * 2^e (m: 가수, 2: 밑수, e: 지수)
부동 소수점(Floating Point) 변환 예시
실수를 부동 소수점 방식으로 저장할 때는 정규화(Normalization) 과정을 거칩니다.
2진수를 정규화하면 1.xxx... * 2^n 형태로 변환됩니다.
2진수의 실수 값에서 정수부에 1만 남을 때까지 소수점을 왼쪽으로 이동시키고 이동한 칸 수만큼 n자리에 표시하면 됩니다.
0.000101이라는 2진수가 있을 때 정수부에 1만 남을 때까지 소수점을 왼쪽으로 이동시켜야 하는데 0.000101에서는 왼쪽에 1이 없다. 정수부에 1을 만들기 위해서는 오른쪽으로 소수점을 옮겨서 1.01 * 2^-4 형태가 된다.
예시로 7.625라는 실수를 2진수로 변환하면 111.101이 되고 이것을 정규화하면 1.11101*2^2가 됩니다.

가수부 자리에는 정규화에서 소수점 오른쪽에 있는 숫자들을 왼쪽부터 채우고 남는 자리는 0으로 채웁니다.
지수부 자리에는 2^n에 해당하는 지수 2의 값에 "Bias"를 더해야 합니다. IEEE 754 형식에서는 32비트는 127, 64비트는 1023의 값을 지수에 더해줘야 합니다.
그러면 지수 2에 127을 더한 129의 값을 2진수로 변환해주면 "10000001" 값이 들어가게 됩니다.
그러면 "Bias"라는 값을 더하는 이유는 지수가 음수가 될 수도 있기 때문이다.
본래 8비트의 표현 가능 숫자의 범위는 -127~128이지만, 지수부에선 부호부가 존재하지 않기 때문에 00000000을 -127로, 11111111을 128로 정의하기로 규정했다고 합니다. 그래서 지수값의 절반을 양의 지수로 절반은 음의 지수로 사용하고자 절반에 해당하는 127을 "Bias"로 규정했습니다.
✔ 부동 소수점 오차
부동 소수점의 오차가 생기는 이유는 위에서 7.625라는 실수의 값을 예시로 들었는데 2진수로 변환하면 111.101이라는 값이 딱 떨어지게 됩니다. 하지만 이런 딱 떨어지는 경우는 흔하지 않습니다.
10진수를 2진수로 변환하는 방법의 그림에서 0.1 실수 값을 2진수로 변환하게 되면 그림에서와 같이 무한소수 값을 확인할 수 있습니다. 이런 무한소수로 인해 가수부에 표현할 수 있는 비트 수를 넘어가게 되면 손실되는 부분이 생기기 때문에 근사치의 값을 넘겨주게 되므로 오차가 발생하게 됩니다.
🔗 Reference
'javascript & typescript' 카테고리의 다른 글
| 동시성(Concurrency) 문제 해결하기 (2) | 2022.10.04 |
|---|
