
BFS가 궁금하면 아래 글을 참조
BFS (Breadth-First Search)
DFS가 궁금하면 아래 글을 참조
DFS (Depth-First Search)
✔ 그래프 이론

그래프는 수학에서 객체 간에 짝을 이루는 관계를 모델링하기 위해 사용되는 수학 구조이다.
그래프(graph)는 아래의 순서쌍으로 볼 수 있다.
$$ G = (V, E) $$
여기서 V는 정점(vertex) 혹은 노드(node)를 의미하고, E는 간선(edge) 혹은 변을 의미한다.
즉, 그래프는 정점 집합과 간선 집합으로 선으로 연결된 구조이다.
✔ 그래프 종류

위 그림은 6개의 노드 7개의 간선을 가지는 그래프이고, 6번 노드의 차수는 1이고, 5번 노드의 차수는 3이다.
이와 같은 그래프를 무향 그래프(무방향 그래프, undirected graph)로 부른다.
- 차수(degree) : 한 노드에 이어져 있는 간선의 수
- 인접(adjacent) : 두 개의 노드 사이에 간선이 존재한다면, 이 두 노드들이 인접한다고 한다(연결이 되어있다)
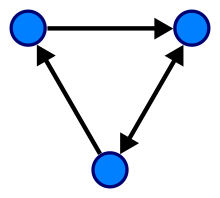
위 그림은 단순 방향 그래프로 유향 그래프(방향 그래프, directed graph)로 방향을 가진 그래프이다.
- 입력 차수(in-degree) : 한 노드로 들어오는 간선의 개수
- 출력 차수(out-degree) : 한 노드에서 나가는 간선의 개수

V1으로 들어오는(in-degree) 간선은 3개, V1에서 나가는(out-degree) 간선 2개이다.
✔ 그래프 구현
그래프 구현에는 인접행렬(Adjacency Matrix), 인접리스트(Adjacency List) 방식이 있다.
- 인접행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- 인접리스트(Adjacency List) : 리스트로 그래프의 연결 관계를 표현하는 방식
1. 인접행렬(Adjacency Matrix)
그래프에서 정점과 간선의 관계를 2차원 배열의 정사각형 행렬로 표현한다.
행, 열은 노드를 의미하고 각각의 원소들은 노드 간의 간선을 표현한다.

연결되어 있는 경우 행렬에서 1의 값을 가지고 연결되지 않은 경우 0의 값을 가진다. 자기 자신 또한 0의 값을 가진다.
1 - 2가 연결되어 있기 때문에 "adj[1][2] = 1"이 되고, 2 - 3은 연결되어 있지 않기 때문에 "adj[2][3]=0"이 된다.
2. 인접리스트(Adjacency List)
그래프에서 정점과 간선의 관계를 연결리스트(Linked List)로 표현한다.
노드 수만큼 인접리스트가 존재하고 인접리스트에 인접한 노드 정보가 저장된다.

1은 2, 3이 연결되어 있기 때문에 "vector<int> adj[1000]" "adj[1].push_back(2)" "adj[1].push_back(3)"이 된다. 리스트로 구현해도 되고 vector로 구현해도 된다.
✔ 공간 복잡도
- 인접행렬(Adjacency Matrix) : $ O(V^2) $
- 인접리스트(Adjacency List) : $ O(V + E) $
✔ 시간 복잡도
1. 한 개의 간선 찾기
- 인접행렬(Adjacency Matrix) : $ O(1) $
- 인접리스트(Adjacency List) : $ O(V) $
2. 모든 간선 찾기
- 인접행렬(Adjacency Matrix) : $ O(V^2) $
- 인접리스트(Adjacency List) : $ O(V + E) $
✔ 인접행렬(Adjacency Matrix) 구현
문제의 범위는 N(5 ≤ N ≤ 25)다.
전체를 탐색해야 하기 때문에 다음의 시간복잡도가 걸린다.
$$ O(N * N) $$
#include <bits/stdc++.h>
const int d4i[]{-1, 0, 1, 0}, d4j[]{0, 1, 0, -1};
int n, c1, c2, ans[626], arr[26][26], vst[26][26];
void dfs(int y, int x) {
c2++;
vst[y][x]=1;
for(int i=0; i<4; ++i) {
int ny=d4i[i]+y, nx=d4j[i]+x;
if(ny<0||ny>=n||nx<0||nx>=n||vst[ny][nx]||!arr[ny][nx]) continue;
dfs(ny, nx);
}
}
int main() {
scanf("%d", &n);
for(int i=0; i<n; ++i)
for(int j=0; j<n; ++j)
scanf("%1d", &arr[i][j]);
for(int i=0; i<n; ++i) {
for(int j=0; j<n; ++j) {
if(arr[i][j]&&!vst[i][j]) {
c2=0;
dfs(i, j);
ans[c1++]=c2;
}
}
}
std::sort(ans, ans+c1);
printf("%d\n", c1);
for(int i=0; i<c1; ++i) printf("%d\n", ans[i]);
return 0;
}
2차원 배열에 지도의 값을 입력받고 DFS로 전체 연결된 컴포넌트의 개수를 구하고 각각의 연결된 컴포넌트의 수를 구하면 되는 문제다.
✔ 인접리스트(Adjacency List) 구현
문제의 범위는 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000)다.
간선 M만큼 N을 탐색해야 하기 때문에 다음의 시간복잡도가 걸린다.
$$ O(MlogN) $$
#include <bits/stdc++.h>
using namespace std;
int n, m, v, a, b, visited[1004];
vector<int> adj[1004];
queue<int> q;
void dfs(int d) {
visited[d]=1;
printf("%d ", d);
sort(adj[d].begin(), adj[d].end());
for(int i : adj[d]) {
if(!visited[i])
dfs(i);
}
}
int main() {
scanf("%d%d%d", &n, &m, &v);
for(int i=0; i<m; ++i) {
scanf("%d%d", &a, &b);
adj[a].push_back(b);
adj[b].push_back(a);
}
dfs(v);
printf("\n");
memset(visited, 0, sizeof(visited));
visited[v]=1;
q.push(v);
while(!q.empty()) {
a=q.front();
q.pop();
printf("%d ", a);
sort(adj[a].begin(), adj[a].end());
for(int i : adj[a]) {
if(!visited[i]) {
visited[i]=1;
q.push(i);
}
}
}
return 0;
}
"vector<int> adj[1004]" 선언하고 입력받은 값을 "adj[a].push_back(b)", "adj[b].push_back(a)"로 인접 리스트에 추가했다. 그리고 DFS로 탐색한다.
🔗 Reference
'algorithm' 카테고리의 다른 글
| 누적합 응용(feat. 2차원 배열) (0) | 2025.02.23 |
|---|---|
| 분배법칙(Distributive Property) (0) | 2025.02.19 |
| 지수법칙 & 모듈러 연산 (0) | 2025.02.13 |
| 누적합(Prefix Sum) (0) | 2025.01.19 |
| DFS (Depth-First Search) (0) | 2023.06.25 |



