✔ 합병 정렬(Merge Sort)
합병 정렬은 퀵 정렬과 마찬가지로 분할 정복(divide and conquer) 방법을 통해 정렬하는 알고리즘이다.
정렬되지 않은 리스트를 각각 하나의 원소만 포함하는 n개의 부분리스트로 분할한다. (한 원소만 든 리스트는 정렬된 것)
분할한 부분리스트를 반복해서 비교하며 병합하여 정렬된 리스트로 만든다.
합병 정렬은 분할, 정복, 결합, 복사의 순으로 이루어진다.
- 분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
리스트의 길이가 1 이하일 때까지 반복한다. - 정복(conquer) : 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. (정렬 결과는 임시 배열에 저장)
- 복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사한다.
분할 정복(divide and conquer)
그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법
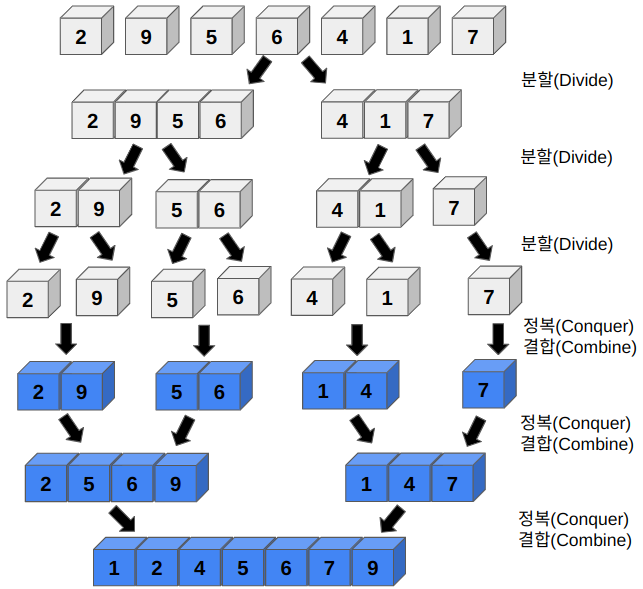
✔ 합병 정렬 동작 과정
- 정렬되지 않은 리스트를 절반으로 나눈다 (리스트의 길이가 1 이하일 때까지 반복)
- 나누어진 부분 리스트를 비교하고 정렬하면서 결합한다 (결합은 임시 배열에 넣는다)
- 임시 배열 데이터를 원본 데이터에 복사한다
- 2번부터 다시 반복하며 하나의 정렬된 리스트로 만든다
✔ 합병 정렬 구현(C++)
#include <iostream>
using namespace std;
const int num = 7;
int sorted[num];
void merge(int * arr, int left, int mid, int right) {
int i = left;
int j = mid+1;
int k = left;
// 작은 순서대로 배열에 삽입(정복 과정)
while(i <= mid && j <= right) {
if(arr[i] <= arr[j]) {
sorted[k++] = arr[i++];
} else {
sorted[k++] = arr[j++];
}
}
// 남은 데이터도 삽입
if(i > mid) {
// 왼쪽부분을 다 정렬시켜 채워넣었다면 오른쪽 부분만 넣으면 된다
for(int l = j; l <= right; ++l) {
sorted[k++] = arr[l];
}
} else {
// 오른쪽부분을 다 정렬시켜 채워넣었다면 왼쪽 부분을 넣으면 된다
for(int l = i; l <= mid; ++l) {
sorted[k++] = arr[l];
}
}
// 정렬된 배열을 삽입
for(int l = left; l <= right; ++l) {
arr[l] = sorted[l];
}
}
void mergeSort(int * arr, int left, int right) {
// 크기가 1보다 큰 경우
if(left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
int main() {
int arr[num] = {2, 9, 5, 6, 4, 1, 7};
mergeSort(arr, 0, num - 1);
for(int i : arr) {
cout << i << " ";
}
return 0;
}
✔ 합병 정렬 시간 복잡도
합병정렬의 시간 복잡도는 아래와 같다.
$$ O(nlogn) $$
분할하고 결합하는 개수가 2배씩 증가한다는 점에서 2 ^ 3 = 8 이므로 순환 호출의 깊이가 3단계이다.
그러므로 단계의 크기는 데이터의 개수가 n개일 때 logn을 유지하게 된다.
또한 정렬 자체에 필요한 수행시간은 n이어서 총 시간 복잡도는 O(nlogn)이 된다.
퀵 정렬은 최악의 경우 O(n^2)의 시간 복잡도이지만, 합병 정렬은 정확히 절반씩 나누기 때문에
최악의 경우에도 O(nlogn)을 보장합니다.
시간 복잡도에 대한 좀 더 자세한 내용은 아래의 내용에서 확인하세요.
시간 복잡도
🔗 Reference
'algorithm' 카테고리의 다른 글
| 큐(Queue) (0) | 2023.05.02 |
|---|---|
| 스택(Stack) (0) | 2023.04.15 |
| 퀵 정렬 알고리즘(Quick Sort) (0) | 2022.12.14 |
| 삽입 정렬 알고리즘(Insertion Sort) (0) | 2022.11.30 |
| 버블 정렬 알고리즘(Bubble Sort) (0) | 2022.11.21 |