·코딩 테스트를 준비하면서 지금까지 알고리즘 문제를 풀 때 시간 복잡도/공간 복잡도 등에 대해서는 생각을 안 하고, 문제를 읽고 해당 문제의 조건으로 구현해서 제출하고 맞으면 다른 사람의 풀이 보고 넘어가고 틀리면 "왜 틀렸지?"라고 막연히 생각만 했었다.
그러다 좋은 강의로 인해 시간복잡도 등 분석에 대해서 알게 되어서 기록 및 공유하고자 한다.
먼저 시간 복잡도에 대해서 간단히 얘기하면,
시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가리킨다.
시간 복잡도는 주로 빅-오 표기법을 사용하여 나타내며, 빅-오 표기법은 계수와 낮은 차수의 항을 제외시키는 방법이다.
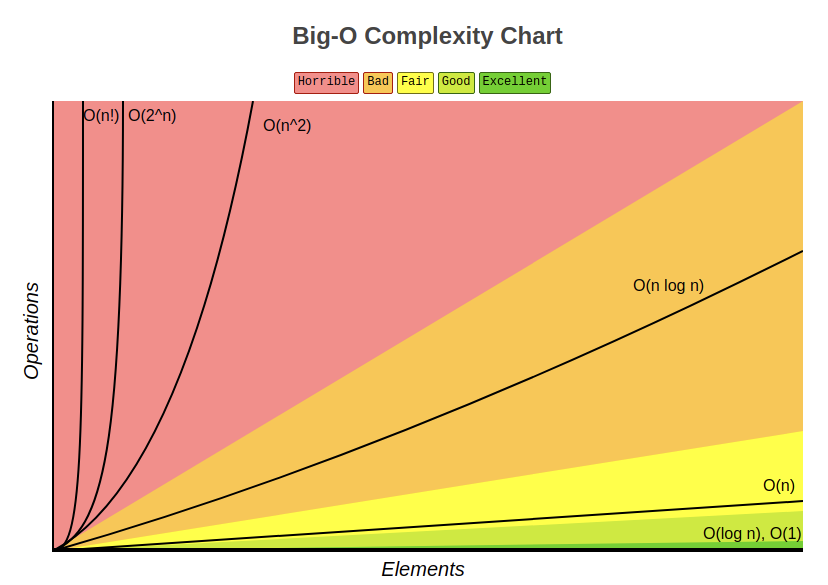
$$ O(N!) > O(2^N) > O(N^2) > O(NlogN) > O(N) > O(\sqrt{N}) > O(logN) > O(1) $$
🔸 O(1)
시간 복잡도 O(1)은 단 하나의 연산이 어떤 배열에서의 요소 위치를 알아내는 것을 수행한다고 할 때, 이 요소에 접근하는 것은 상수 시간(O(1))이 걸린다.
ex) 예시
1부터 N까지 합을 구하는 알고리즘.
def sum(n):
ret = 0
for i in range(1, n+1):
ret += i
return ret위와 같이 1부터 N까지 반복하면서 더해서 구할수도 있지만, 이러면 시간 복잡도는 O(N)이다.
입력 값 N의 길이에 비례하는 시간을 요구하기 때문이다.
def sum(n):
return n * (n+1) // 2하지만 위와 같이 하나의 수식으로 연산하면 시간복잡도는 O(1)이다.
🔸 O(N)
시간 복잡도 O(N)은 큰 입력 값에 대해서 수행시간이 입력 값에 따라 선형적으로 증가함을 의미한다.
ex) 예시
길이 N 수열에서 수 K 찾기(sum, max, min도 유사)
def search(lst, k):
for i in lst:
if i == k: return True
return False위와 같은 경우 입력 값이 N개인 수열에서 k를 찾을려면 최악의 경우 N번을 돌려봐야 한다.
최선의 경우에는 한 번만에 찾을 수 있지만, 최선의 경우일 때는 가능하지만 최악일 때는 안될 수도 있기 때문이다.
🔸 O(logN)
시간 복잡도 O(logN)은 인스턴스당 연산이 각 인스턴스에 대해서 최대한 줄어드는 것이 필요하기 때문에, 높은 효율을 갖고 있다.
ex) 예시
길이 N 수열에서 수 K 찾기(이진탐색)
단, 정렬이 되어 있고, 0~9에서 3을 찾는다고 가정
def solution(lst, k):
lo, hi = 0, len(lst)-1
while lo <= hi:
mid = (lo+hi) // 2
if lst[mid] == k: return mid
if lst[mid] > k: hi = mid-1
else: lo = mid+1
return -1위와 같이 계속 길이가 절반으로 줄어든다.
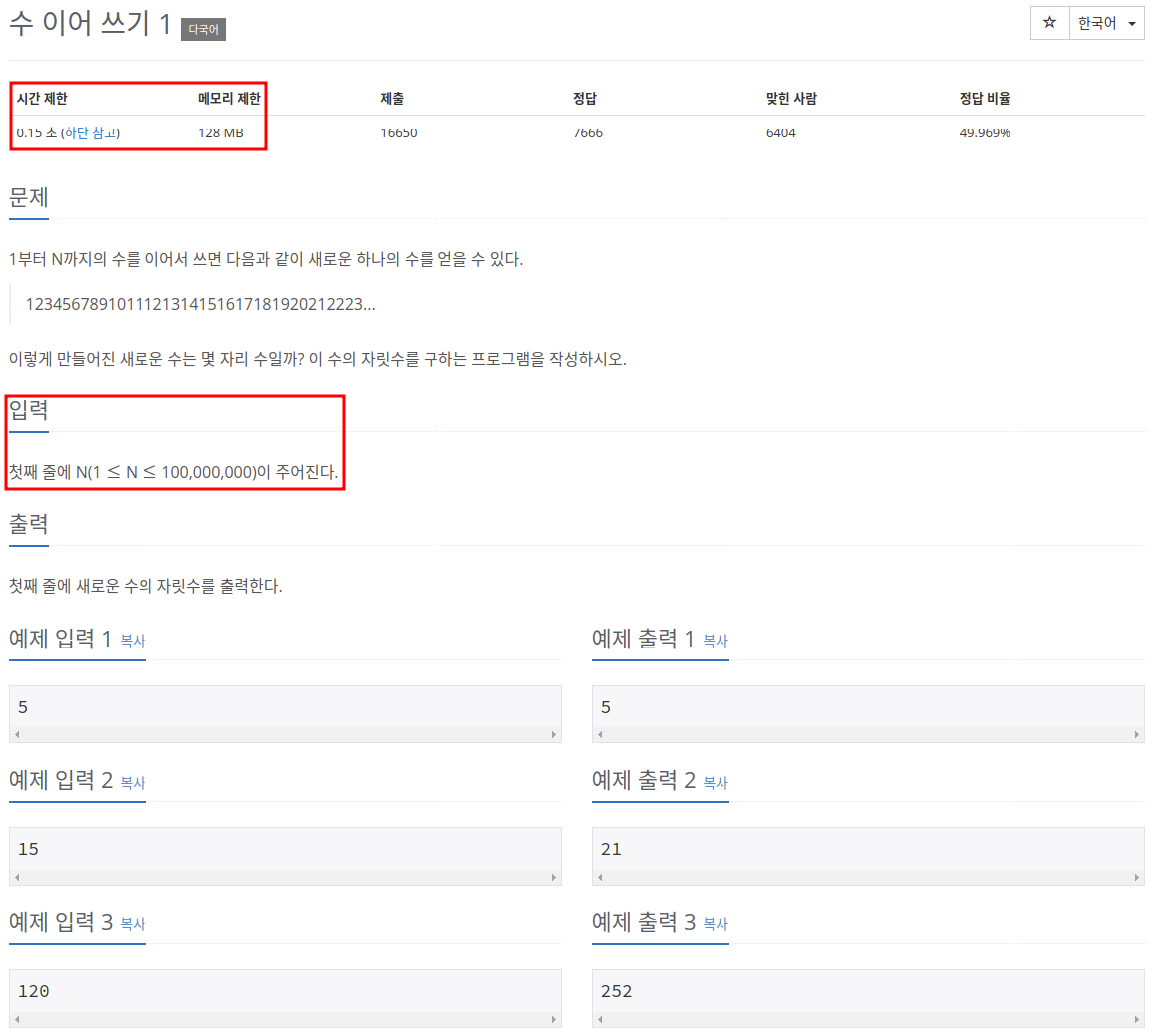
위의 문제는 문제를 떠나서 0.15초 제한에 max(N) = 10억이기 때문에 O(N) 이상의 알고리즘은 모두 불가능하다고 한다.
풀이 방식은 본인이 생각하는 가장 쉬운 풀이를 떠올리고, 그 다음에 알고리즘에서 중복되는 코드를 줄일 수 있는 방법을 생각한다.
◼ 기본적인 풀이
def solution(n):
ret = 0
for i in range(1, n+1):
ret += len(str(i))
return ret
# Pythonic으로 변경
def solution(n):
return sum(map(lambda x: len(str(x)), range(1, n+1)))위의 방식은 시간 복잡도 O(NlogN)에 해당한다. 이유는 N은 반복문, logN은 str연산이다.
◼ 중간 과정에 반드시 필요한 로직 생각하기
먼저 ret += len(str(i)) 로직에 해당하는 수의 길이를 구하는 방법을 생각해본다.
- 일의 자리수(10으로 나눈 나머지)와
- 나머지 수(10으로 나눈 값)로 나누기
- 0이 되는 순간 과정 끝
- 10씩 나누면 되니 log10N번의 연산으로 가능
def num_len(n):
ret = 0
while n:
n /= 10
ret += 1
return ret◼ 예제 입출력 매칭해서 최종 로직 생각하기
예제 입력3: 120 / 예제 출력3: 252
- 1,2,3···8,9
- 10,11,12···98,99
- 100,101,102···119,120
120까지 숫자를 이어쓰면
1의 자리 9개, 2의 자리 90개, 3의 자리 21개 = 9 + 180 + 63 = 252
def solution(n):
l, ret = len(str(n)), 0
for i in range(1, l): # l-1 자리 수의 값을 구한다
ret += i * (10**i - 10**(i-1))
ret += l * (n - 10**(l-1) + 1) # l의 자리 수 값을 구한다
return ret
📌 Reference
'algorithm' 카테고리의 다른 글
| 선택 정렬 알고리즘(Selection Sort) (0) | 2022.11.09 |
|---|---|
| [Algorithm] 소수 구하기 (0) | 2022.04.05 |
| 하노이 탑 이동 순서 (0) | 2021.04.12 |
| 피보나치 수열 알고리즘 (0) | 2021.04.04 |
| [Algorithm] 최대공약수(GCD), 최소공배수(LCM) (0) | 2021.04.04 |



