BFS (Breadth-First Search)

DFS가 궁금하면 아래 글을 참조
DFS (Depth-First Search)

✔ BFS(Breadth-First Search)

BFS는 너비 우선 탐색이라고도 부르며, 그래프를 탐색하는 방법 중 하나이다.

하나의 정점으로부터 시작해서 차례대로 모든 정점들을 한 번씩 방문하는 것으로 즉, 시작 노드에서 출발해 인접한 노드(가까운 노드)를 먼저 탐색하고 현재 깊이의 모든 노드를 탐색하면서 가는 알고리즘이다.

깊게 탐색하기 전에 넓게 탐색
두 정점 사이의 최단 경로를 구할 때 사용
같은 가중치를 가진 그래프에서 사용
큐(queue)를 사용하여 구현

※ 중요한 점은 방문한 정점은 다시 방문하지 않아야 한다.

만약 가중치가 다른 그래프일 때 최단거리를 구하는 알고리즘은 다익스트라, 벨만포드 등으로 구현해야 한다.

BFS로 탐색하는 것은 레이어별, 깊이별로 탐색하는 것이다.

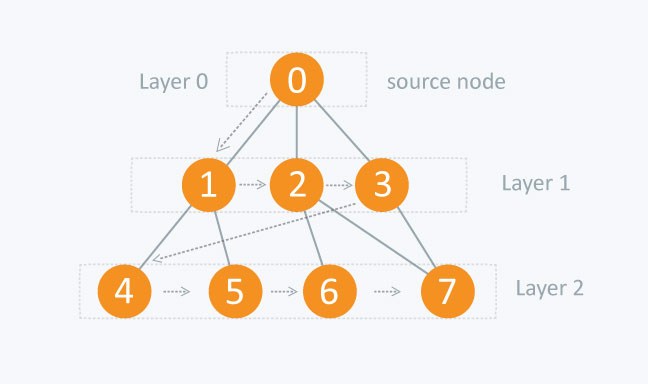
BFS와 DFS의 탐색 방법 차이는 아래와 같다.

✔ BFS 동작 과정

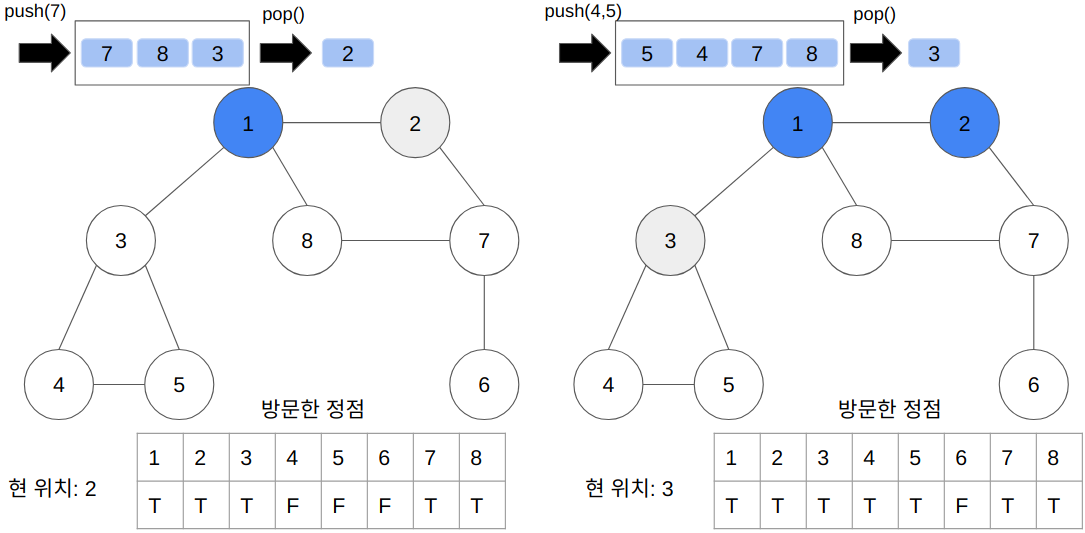
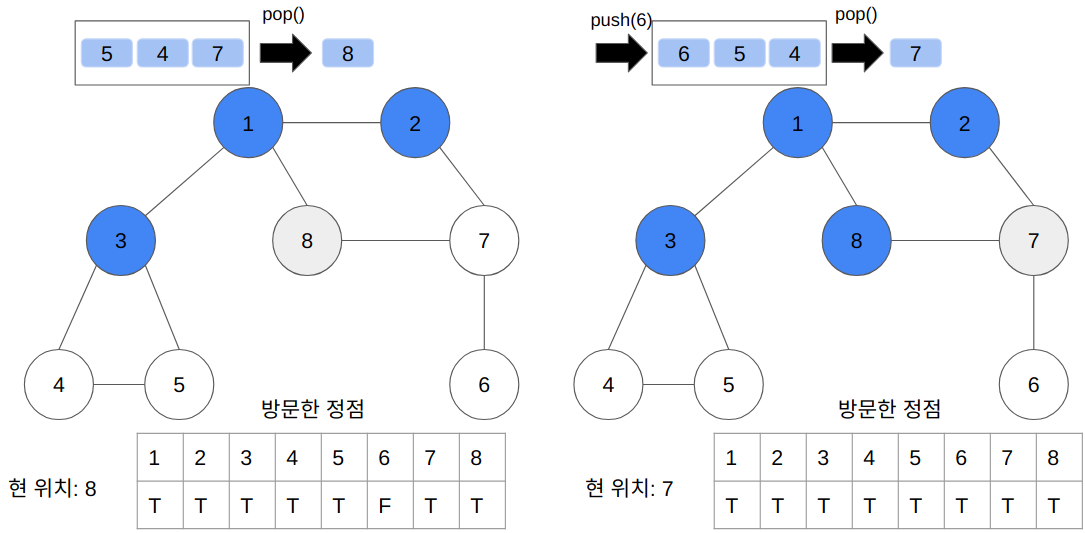
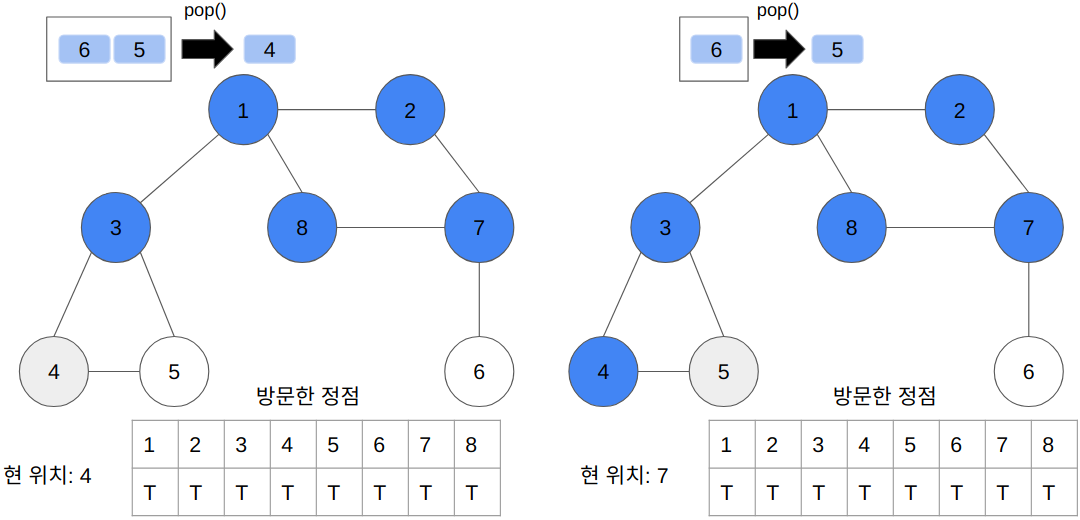
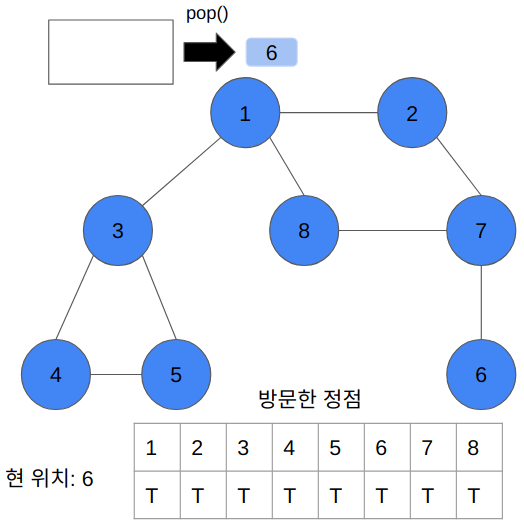
전체 탐색 순서
- 1 → 2 → 3 → 8 → 7 → 4 → 5 → 6

큐가 빌 때까지 반복해서 진행하면 된다.

시작 노드인 "1" 큐에 넣고 방문 등록
큐의 첫 번째 값 "1" 가져오고 "1" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 2, 3, 8 정점 삽입 & 해당 정점들을 방문 표시
큐의 첫 번째 값 "2" 가져오고 "2" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 7 정점 삽입 & 방문 표시 / 1 정점은 이미 방문을 했기 때문에 패스
큐의 첫 번째 값 "3" 가져오고 "3" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 4, 5 정점 삽입 & 방문 표시 / 1 정점은 이미 방문을 했기 때문에 패스
큐의 첫 번째 값 "8" 가져오고 "8" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 1, 7 정점 모두 이미 방문을 했기 때문에 패스
큐의 첫 번째 값 "7" 가져오고 "7" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 6 정점 삽입 & 방문 표시 / 2, 8 정점은 이미 방문을 했기 때문에 패스
큐의 첫 번째 값 "4" 가져오고 "4" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 3, 5 정점 모두 이미 방문을 했기 때문에 패스
큐의 첫 번째 값 "5" 가져오고 "5" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 3, 4 정점 모두 이미 방문을 했기 때문에 패스
큐의 첫 번째 값 "6" 가져오고 "6" 연결된 정점들을 방문했는지 확인, 방문하지 않았으면 큐에 삽입
1. 7 정점 이미 방문을 했기 때문에 패스
큐가 모두 비어서 종료

✔ BFS 구현(C++)

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

vector<vector<int>> vertex={
    {},
    {2, 3, 8},
    {1, 7},
    {1, 4, 5},
    {3, 5},
    {3, 4},
    {7},
    {2, 6, 8},
    {1, 7}
};
vector<int> visited(9, 0);
void bfs(int n) {
    queue<int> q;
    q.push(n);
    visited[n]=1;
    while(!q.empty()) {
        int cur = q.front();
        q.pop();
        cout << cur << " ";
        for(auto i : vertex[cur]) {
            if(!visited[i]) {
                visited[i] = 1;
                q.push(i);
            }
        }
    }
    return;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    bfs(1);
    return 0;
}

✔ BFS 시간 복잡도

인접 리스트로 표현된 그래프에서는 정점(Vertex), 간선(Edge)에 영향을 받으므로 아래와 같다.

$$ O(V + E) $$

인접 행렬로 표현된 그래프에서는 아래와 같다.

$$ O(V^2) $$

✔ BFS 문제

출처 - 백준 2178번 미로 탐색

미로 탐색은 맵을 주고 시작 정점에서 도착 정점까지의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 문제이다.

최소의 칸 수 즉, 최단 거리를 구해야 하기 때문에 BFS를 구현해서 풀어주면 된다.

#include <iostream>
#include <queue>
#include <tuple>
using namespace std;

const int d4i[4]={-1, 0, 1, 0}, d4j[4]={0, 1, 0, -1};
int n, m, y, x, arr[104][104], visited[104][104];
int main() {    
    scanf("%d %d", &n, &m);
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < m; ++j)
            scanf("%1d", &arr[i][j]);

    queue<pair<int, int>> q;
    q.push({0, 0});
    visited[0][0] = 1;
    
    while(!q.empty()) {
        tie(y, x) = q.front();
        q.pop();
        
        for(int i = 0; i < 4; ++i) {
            int ny = y + d4i[i];
            int nx = x + d4j[i];
            
            if(ny < 0 || ny >= n || nx < 0 || nx >= m) continue;
            if(!arr[ny][nx] || visited[ny][nx]) continue;
            
            visited[ny][nx] = visited[y][x] + 1;
            q.push({ny, nx});
        }
    }
// 디버깅용 출력(2차원 배열에 움직이는 수 표시)
//    for(int i = 0; i < n; ++i) {
//        for(int j = 0, j < m; j++)
//            printf("%d ", visited[i][j]);
//        printf("\n");
//    }
    printf("%d", visited[n-1][m-1]);
    return 0;
}

BFS를 공부하고 느낀 점은 위의 BFS에 대한 내용 자체는 어렵지 않았다.

하지만 알고리즘 문제를 읽고 그 문제를 BFS로 구현하면 되겠다고 생각하는 점과, 문제마다 내용이 다르기 때문에

BFS를 응용해서 구현해야 한다는 점이 문제를 많이 경험하지 않는 사람에게는 어려운 것 같다고 생각이 들었다.

🔗 Reference

'Algorithm' 카테고리의 다른 글

DFS (Depth-First Search) (0)	2023.06.25
큐(Queue) (0)	2023.05.02
스택(Stack) (0)	2023.04.15
합병 정렬 알고리즘(Merge Sort) (0)	2023.01.10
퀵 정렬 알고리즘(Quick Sort) (0)	2022.12.14

슈뢰딩거의 고양이

BFS (Breadth-First Search)