DFS (Depth-First Search)

BFS가 궁금하면 아래 글을 참조
BFS (Breadth-First Search)

✔ DFS(Depth-First Search)

DFS는 깊이 우선 탐색이라고도 부르며, 그래프를 탐색하는 방법 중 하나이다.

하나의 정점으로부터 시작해 차례대로 모든 정점들을 한 번씩 방문하는 것으로 즉, 시작 노드에서 출발해 인접한 노드(가까운 노드)를 먼저 탐색하고 그 정점의 최대 깊이까지 탐색을 마친 후 돌아와 다른 분기로 다시 탐색하는 알고리즘이다.

넓게 탐색하기 전에 깊게 탐색
스택 or 재귀를 사용하여 구현
모든 노드를 방문할 때 사용

※ 중요한 점은 방문한 정점은 다시 방문하지 않아야 한다.

DFS는 스택으로도 구현할 수 있지만 재귀로 구현하는 편이 더 깔끔해서 재귀로 더 많이 구현하는 것 같다.

DFS와 BFS의 탐색 방법 차이는 아래와 같다.

✔ DFS 동작 과정(재귀)

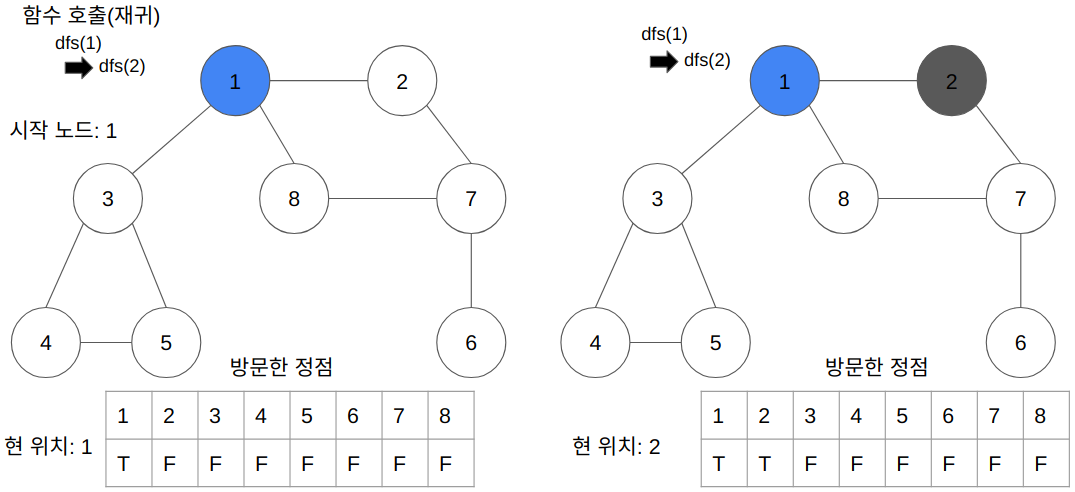
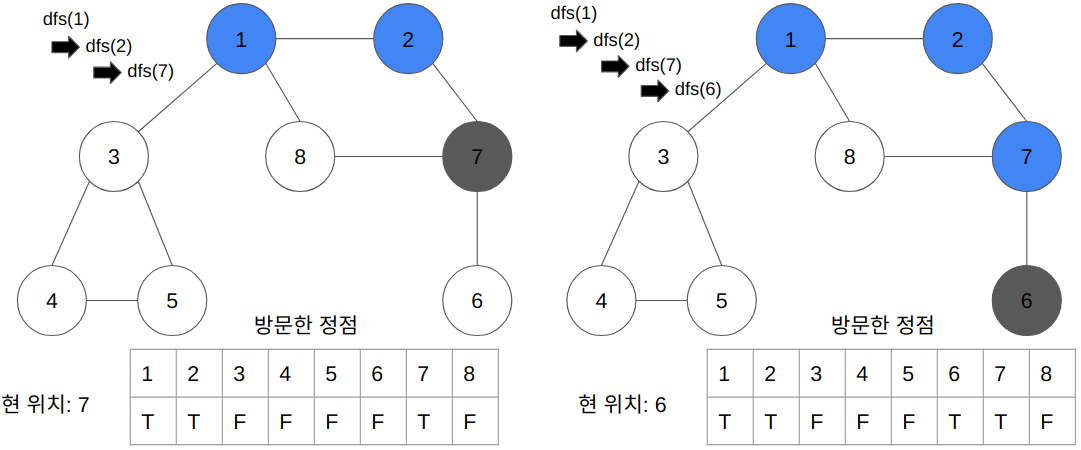
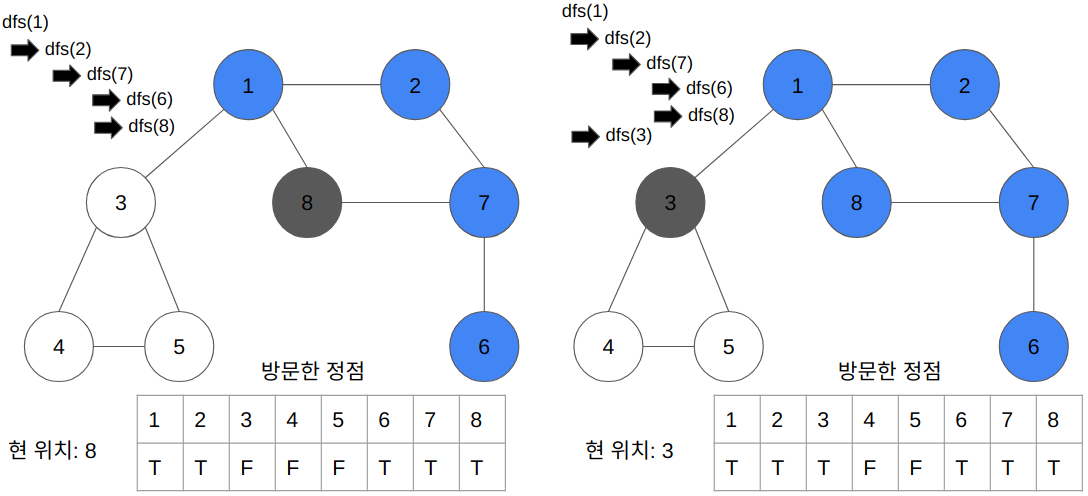
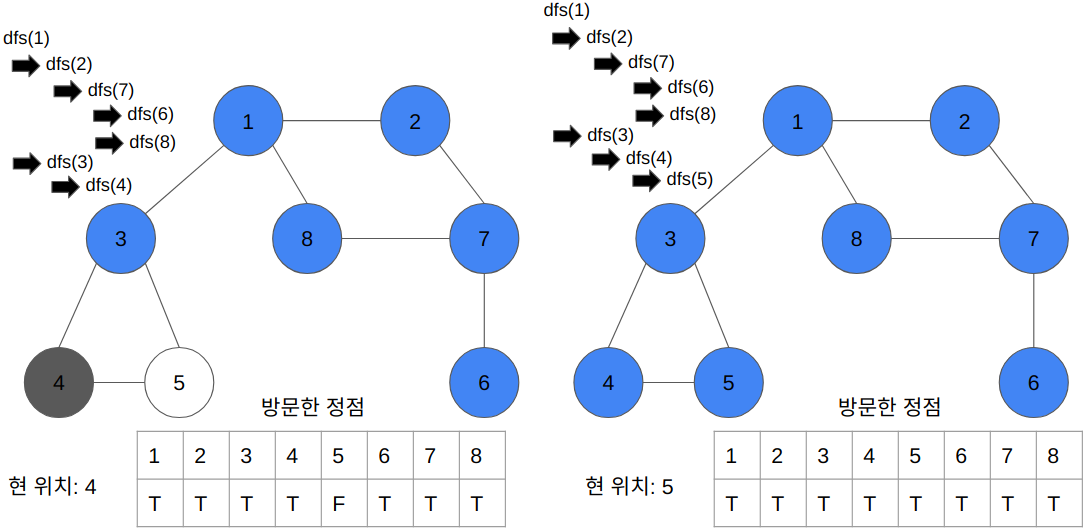
전체 탐색 순서
- 1 → 2 → 7 → 6 → 8 → 3 → 4 → 5

모든 정점을 다 방문할 때까지 진행된다.

인접 리스트 목록에서 인접한 정점들이 오름차순으로 정렬된 상태

시작 정점인 "1" 인수값으로 dfs 함수 호출
1. 1 정점 방문 표시 & 1 정점 인접 리스트를 찾는다
"1" 정점 인접 리스트에 있는 "2" 인수값으로 dfs 함수 호출
1. 2 정점 방문 표시 & 2 정점 인접 리스트를 찾는다(1 정점은 이미 방문했으므로 패스)
"2" 정점 인접 리스트에 있는 "7" 인수값으로 dfs 함수 호출
1. 7 정점 방문 표시 & 7 정점 인접 리스트를 찾는다(2 정점은 이미 방문했으므로 패스)
"7" 정점 인접 리스트에 있는 "6" 인수값으로 dfs 함수 호출
1. 6 정점 방문 표시 & 6 정점 인접 리스트를 찾는다(7 정점은 이미 방문했으므로 패스)
"6" 정점 인접 리스트에는 더 이상할 수 있는 게 없으므로 리턴돼서 함수를 빠져나온다
1. 6 정점을 호출한 7 정점으로 돌아간다
"7" 정점 인접 리스트에 있는 "8" 인수값으로 dfs 함수 호출
1. 8 정점 방문 표시 & 8 정점 인접 리스트를 찾는다(1, 7 정점은 이미 방문했으므로 패스)
"8" 정점 인접 리스트에는 더 이상할 수 있는 게 없으므로 리턴돼서 함수를 빠져나온다
1. 7 정점으로 빠져나오고 7 정점에서도 더 할 게 없으므로 리턴되고 2 정점도 빠져나오고 1 정점으로 되돌아간다
"1" 정점 인접 리스트에 있는 "3" 인수값으로 dfs 함수 호출
1. 3 정점 방문 표시 & 3 정점 인접 리스트를 찾는다(1 정점은 이미 방문했으므로 패스)
"3" 정점 인접 리스트에 있는 "4" 인수 값으로 dfs 함수 호출
1. 4 정점 방문 표시 & 4 정점 인접 리스트를 찾는다(3 정점은 이미 방문했으므로 패스)
"4" 정점 인접 리스트에 있는 "5" 인수 값으로 dfs 함수 호출
1. 5 정점 방문 표시 & 5 정점 인접 리스트를 찾는다(1, 4 정점은 이미 방문했으므로 패스)
"5" 정점 인접 리스트에는 더 이상할 수 있는 게 없으므로 리턴돼서 함수를 빠져나온다
1. 모든 정점을 다 방문했으므로 함수를 다 빠져나오면서 종료

✔ DFS 동작 과정(스택)

스택으로 하는 방법은 재귀랑 크게 다르지 않지만 다른 점은 재귀 함수는 하나씩 호출하기 때문에 방문하는 정점의 순서가 달라진다. 스택으로 할 때는 해당 정점의 인접한 리스트를 먼저 모두 스택에 넣고 스택에서 뺀 정점을 방문하기 때문에 순서가 달라진다는 점이다.

위의 그림을 스택으로 표현했을 때의 순서는 다음과 같다.

전체 탐색 순서
- 1 → 8 → 7 → 6 → 3 → 5 → 4 → 2

✔ DFS 재귀 구현(C++)

#include <iostream>
#include <vector>
using namespace std;

vector<vector<int>> vertex={
    {},
    {2, 3, 8},
    {1, 7},
    {1, 4, 5},
    {3, 5},
    {3, 4},
    {7},
    {2, 6, 8},
    {1, 7}
};
vector<int> visited(9, 0);

void dfs(int n) {
    visited[n] = 1;
    cout << n << " ";
    for(auto i : vertex[n])
        if(!visited[i])
            dfs(i);
    return;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    dfs(1);
    return 0;
}

✔ DFS 스택 구현(C++)

#include <iostream>
#include <vector>
#include <stack>
using namespace std;

vector<vector<int>> vertex={
    {},
    {2, 3, 8},
    {1, 7},
    {1, 4, 5},
    {3, 5},
    {3, 4},
    {7},
    {2, 6, 8},
    {1, 7}
};
vector<int> visited(9, 0);

void dfs(int n) {
    stack<int> stk;
    visited[n] = 1;
    stk.push(n);
    while(!stk.empty()) {
        int x = stk.top();
        stk.pop();
        cout << x << " ";
        for(auto i : vertex[x]) {
            if(!visited[i]) {
                visited[i] = 1;
                stk.push(i);
            }
        }
    }
    return;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    dfs(1);
    return 0;
}

✔ DFS 시간 복잡도

인접 리스트로 표현된 그래프에서는 정점(Vertex), 간선(Edge)에 영향을 받으므로 아래와 같다.

$$ O(V+E) $$

인접 행렬로 표현된 그래프에서는 아래와 같다.

$$ O(V^2) $$

✔ DFS 문제

출처 - 백준 2606번 바이러스

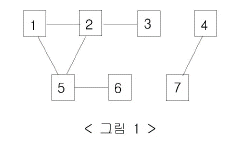
그림 1과 같은 네트워크 상에서 연결되어 있을 때 웜 바이러스는 네트워크를 통해 전파된다.

1번 컴퓨터를 통해 웜 바이러스에 걸리게 되는 컴퓨터의 수를 출력하는 문제이다.

1번과 연결된 컴포넌트를 찾아주면 되는데 DFS를 구현해서 풀어주면 된다.

#include <iostream>
#include <vector>
using namespace std;

int n, m, a, b, visited[104], cnt=-1;
vector<vector<int>> v;

void dfs(int n) {
    cnt++;
    visited[n] = 1;
    for(int i : v[n]) {
        if(!visited[i])
            dfs(i);
    }
    return;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> m;
    v.resize(n+1);
    for(int i = 0; i < m; ++i) {
        cin >> a >> b;
        v[a].push_back(b);
        v[b].push_back(a);
    }
    dfs(1);
    cout << cnt;
    return 0;
}

🔗 Reference

'algorithm' 카테고리의 다른 글

지수법칙 & 모듈러 연산 (0)	2025.02.13
누적합(Prefix Sum) (0)	2025.01.19
BFS (Breadth-First Search) (1)	2023.06.17
큐(Queue) (0)	2023.05.02
스택(Stack) (0)	2023.04.15

슈뢰딩거의 고양이

DFS (Depth-First Search)