✔ 에라토스테네스의 체
수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.
✔ 알고리즘
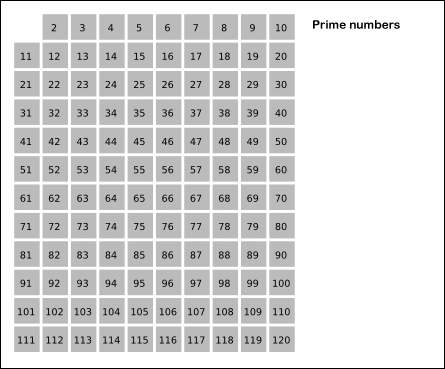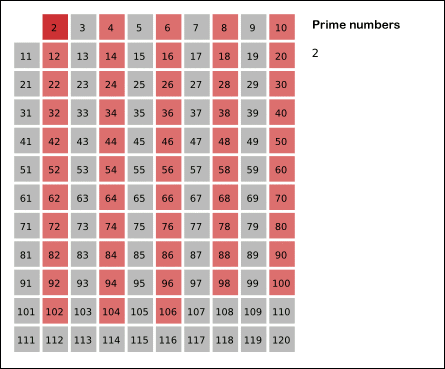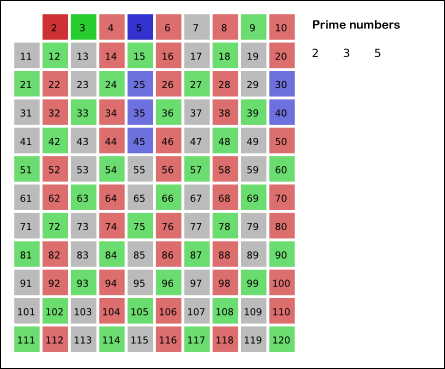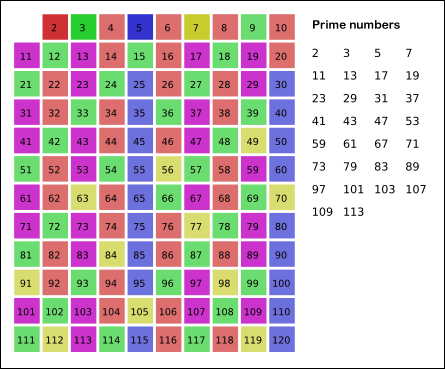
에라토스테네스의 체 방식은 위와 같이 2부터 시작해 해당 배수의 값을 지워 나가면 된다.
에라토스테네스의 시간 복잡도는 O(nloglogn) 이다.
사실 O(nloglogn)이 어느 정도인지 모르겠다... 다만, O(n)인 선형 알고리즘보다 빠르다고 생각하고 있다.
배수의 값을 미리 지우기 때문이라고 생각한다.(DP 느낌? 👀)
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n=120, cnt=0;
vector<bool> v(n+1, 1);
for(int i=2; i*i<=n; ++i) {
if(v[i])
for(int j=i*i; j<=n; j+=i)
v[j] = 0;
}
for(int i=2; i<=n; ++i) {
if(v[i])
cnt++;
}
cout << "120까지의 소수 개수: " << cnt << "\n";
return 0;
}📌 Reference
'algorithm' 카테고리의 다른 글
| 버블 정렬 알고리즘(Bubble Sort) (0) | 2022.11.21 |
|---|---|
| 선택 정렬 알고리즘(Selection Sort) (0) | 2022.11.09 |
| [Algorithm] 알고리즘 읽기와 분석(시간복잡도) (0) | 2022.03.16 |
| 하노이 탑 이동 순서 (0) | 2021.04.12 |
| 피보나치 수열 알고리즘 (0) | 2021.04.04 |



