✔ 하노이 탑
하노이의 탑에는 크기가 다른 원반이 n개 있고 원반을 끼울 수 있는 기둥이 세 개 있다.
하노이의 탑 문제는 어떻게 하면 원반 n개를 모두 가장 왼쪽 기둥(출발점, 1번 기둥)에서 오른쪽 기둥(도착점, 3번 기둥)으로 옮길 수 있을까 하는 문제이다.
※ 하노이 탑 규칙
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력. 단, 이동 횟수는 최소가 되어야 한다.
✔ 하노이 탑 풀이
- 원반이 3개일 때
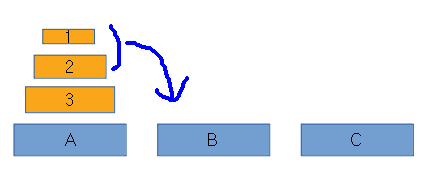
원반 전체를 'C'로 옮기려면, 3원반이 'C'로 먼저 옮겨져야 하니깐, 1,2원반이 'B'로 옮겨져야 한다.
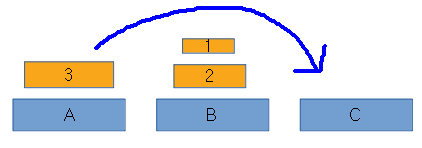
그러면 위와 같이 3원반을 'C'로 옮길 수 있다.
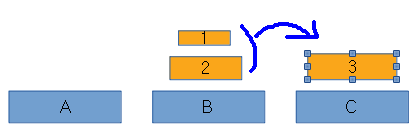
이제 'B'에 있는 1,2원반을 'C'로 옮긴다.
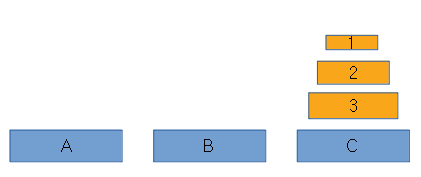
이런식으로 원반 옮기기가 진행된다.
그러면 위의 내용을 정리하자면
- 원반이 n개일 때
- 1번 기둥에 있는 n-1개 원반을 2번 기둥으로 옮긴다.
- 1번 기둥에 남아 있는 가장 큰 원반을 3번 기둥으로 옮긴다.
- 2번 기둥에 있는 n-1개 원반을 3번 기둥으로 옮긴다.
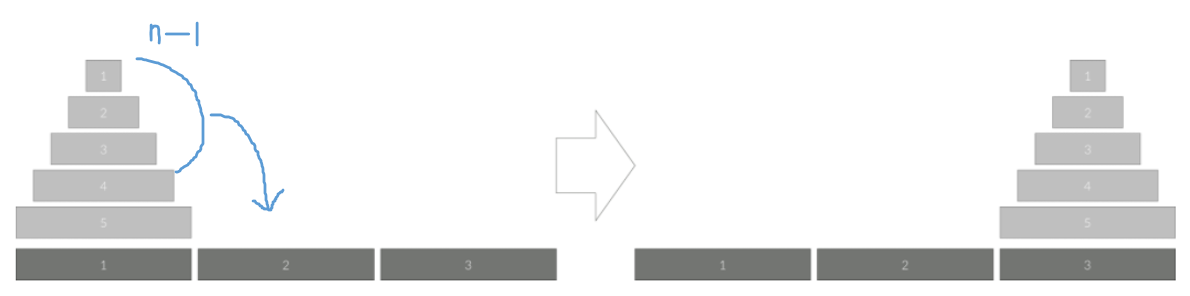
✔ 하노이 탑 알고리즘
※하노이 탑 조건
- 원반이 한 개면 그냥 옮기면 끝(종료 조건)
- 원반이 n개일 때
1. 1번 기둥에 있는 n개 원반 중 n-1개를 2번 기둥으로 옮긴다(3번 기둥 활용)
2. 1번 기둥에 남아 있는 가장 큰 원반을 3번 기둥으로 옮긴다
3. 2번 기둥에 있는 n-1개 원반을 다시 3번 기둥으로 옮긴다(1번 기둥 활용)
def hanoi(n, from, by, to):
if n == 1:
print(from, to)
return
# 원반 n-1개를 1번 기둥에서 2번 기둥으로 이동
hanoi(n-1, from, to, by)
# 큰 원반 1개를 1번 기둥에서 3번 기둥으로 이동
print(from, to)
# 작은 원반 n-1개를 2번 기둥에서 3번 기둥으로 이동
hanoi(n-1, by, from, to)
hanoi(3, 'A', 'B', 'C')n의 값이 4층이면 15, 5층이면 31번을 이동해야 한다.
n층짜리 하노이 탑을 옮기려면 원반을 몇 번 움직여야 할까?
$2^{n}-1$ 번 옮겨야 한다. n이 커지면 -1은 큰 의미가 없으므로 O($2^n$)으로 표현할 수 있다.
이는 2를 n번 제곱한 값이므로 n이 커짐에 따라 값이 기하급수적으로 증가한다.
✔ 계산 복잡도
- O(1) : n과 무관하게 일정한 시간이 걸림.
- O(logn) : n의 log에 비례하여 계산이 증가.
- O(n) : n과 비례하여 계산 시간이 증가.
- O($n^2$) : n의 제곱에 비례하여 계산 시간이 증가.
- O($2^n$) : 2의 n 제곱에 비례하여 계산 시간이 증가.
'algorithm' 카테고리의 다른 글
| 선택 정렬 알고리즘(Selection Sort) (0) | 2022.11.09 |
|---|---|
| [Algorithm] 소수 구하기 (0) | 2022.04.05 |
| [Algorithm] 알고리즘 읽기와 분석(시간복잡도) (0) | 2022.03.16 |
| 피보나치 수열 알고리즘 (0) | 2021.04.04 |
| [Algorithm] 최대공약수(GCD), 최소공배수(LCM) (0) | 2021.04.04 |


